Recurse Center Day 15: B Tree Algorithms
This is a draft post that I have prematurely published. Currently, I am attending RC and I want to write as much as possible, log my daily learnings and activities. But, I also don't want to spend time on grammar and prose, so I am publishing all the posts which usually I'd have kept in my draft folder.
NOTE: I feel that the following is unclear unless someone first reads the CLRS book. I will expand this article later and try to make it less dependent on the book.
B Tree Algorithms
I spent some more time understanding the insertion (and also, search) algorithm. I won’t be implementing deletion with rebalancing because, over time, the deleted spots in the node will get filled with new insertions.
Assumptions:
- Only keys are being inserted, as opposed to key value pairs.
- The book uses 1 based indexing; the following is 0 based
Also, following isn’t a fully working Python code, and I have skipped many explicit parts because understanding the algorithm was my goal.
Initialisation
At first, we don’t have a tree or a node. We create a new leaf node, use that as a root. In a B Tree, the root starts a leaf.
class BTree():
def __init__(self, root: Node, max_keys: int = 7):
self.root = root
# the number of maximum keys each node this B Tree can have
self.max_keys = max_keys
class Node():
def __init__(self):
self.keys: List[int] = []
self.children: List[Node] = []
self.isLeaf = False
# if the Node is full, then it will have `max_keys` number of keys and `max_keys+1` children
def is_full(self) -> bool:
pass
def create() -> BTree:
root: Node = getNewLeafNode()
return BTree(root)
b_tree = create()
Split Node
The split node takes a parent and a child, which is full, to be split. Illustration from the book:
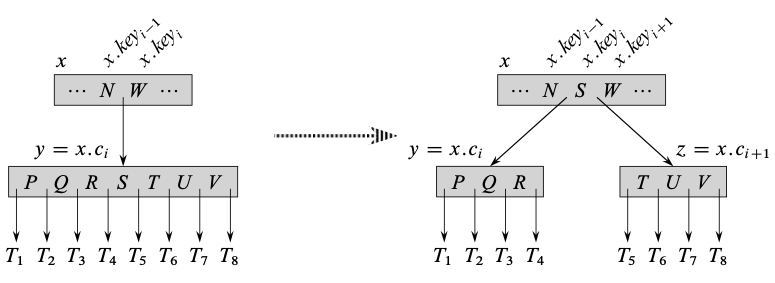
Before calling split_node, we need to make sure that the parent node is not full. If it is full, then it needs to be split as well, which ensures that we are not going crazy with recursion and we are splitting top down:
# this method takes the parent which has a full child, which needs to be split
# `child_index` param gives the position of child node in `parent.children` array
def split_child(btree: BTree, parent: Node, child_index: int):
old_child: Node = parent[child_index]
new_child: Node = getNewNode()
new_child.isLeaf = old_child.isLeaf
split_point = int(btree.max_keys//2)
# copies second half of old child to new one
for i in range(split_point+1, btree.max_keys):
new_child.keys.append(old_child.keys[i])
# if old_child is internal (i.e. isLeaf is false), copy the pointers
# to the new child
if not old_child.isLeaf:
for i in range(split_point+1, btree.max_keys+1):
new_child.children.append(old_child.children[i])
median = old_child[split_point]
# insert the key at the right position
parent.keys.insert(child_index, median)
# insert the new child in the parent
parent.children.insert(child_index+1, new_child)
old_child.keys = old_child.keys[:split_point]
Insertion
We will do the insertion as explained earlier. The insertion starts will splitting of root if it is full:
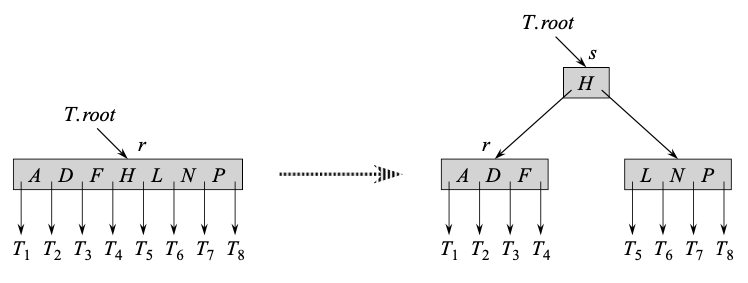
def insert(b_tree: BTree, key: int):
root = b_tree.root
if root.is_full():
# root is full already, so we will split and create
# a new root
new_root = getNewNode()
b_tree.root = new_root
# old root becomes first child of new root
new_root.keys[0] = root
# old root is at 0 position, it needs to be split. So we will call `split_child`
split_child(new_root, 0)
# now we know it is not full, so we go on and insert into it
insert_non_full(new_root, k)
else:
# the root has empty space, so we can insert into it easily
insert_non_full(root, k)
We use insert_non_full to insert in a node that has space in case the child splits.
def insert_non_full(node: Node, key: int):
# if the node is a leaf node, then we
# can insert in it directly. We know it's not full.
if node.isLeaf:
# insert in the node at right place
return
# the node is an internal node. so we find an appropriate place to insert
# it is possible that the child node we picked is full already. So, we will call split_node on it and then insert
# TODO: find the child node to insert; it should be key < child.key
child = node.children[i]
if child.is_full():
split_child(node, i)
insert_non_full(child, key)
Note that the node format here follows the book instead of the one I described earlier. During the split, you need to adjust the parent array like this:
[(7, *1), (16, *9)]
if node 16 gets split, it could look like this:
[(7, *1), (13, *9) (16, *14)]
13 is the key promoted from the child node, which points to the older node (*9), and the earlier 16 now points to the new split child (*14).
Coffee Chat
I had a Coffee Chat with James, who is also one of the faculty. We talked about various things, from books to distributed systems. James also gave me advice on pairing effectively:
- If the task is complicated, requires lots of background reading (which is somewhat true in the case of B Tree), it is better to pair with the same people repeatedly or have a long term pairing partner.
- Split the task into so small that it does not require much background. E.g. writing unit tests.
People
I paired with Oliver to implement split_child. Pairing on this turned out to be very helpful to me because Oliver is used to reading papers and math notations, so turning the algorithm into pseudocode was very quick.